周志华《机器学习》习题解答：Ch5.5 - BP算法实现

基于pybrain包分别实现标准BP算法与累积BP算法，针对西瓜数据集进行了实验并比较了结果。

这里的编程基于Python-PyBrain。Pybrain是一个以神经网络为核心的机器学习包，相关内容可参考神经网络基础 - PyBrain机器学习包的使用，源代码托管于Github：PnYuan/Machine-Learning_ZhouZhihua，欢迎访问.

问题回顾

编码基于Python实现，整个实验过程如下：（这里查看完整代码和数据集）：

step 1.基于PyBrain分别实现标准BP和累积BP两种算法下的BP网络训练，并进行比较；

解题过程

算法分析

参考书上推导及算法图5.8，首先给出BP算法的两种版本示意如下：

Algorithms 1. 标准BP算法
----
    输入： 训练集 D，学习率 η.
    过程： 
        1. 随即初始化连接权与阈值 (ω，θ).
        2. Repeat：
        3.   for x_k，y_k in D:
        4.     根据当前参数计算出样本误差 E_k.
        5.     根据公式计算出随机梯度项 g_k.
        6.     根据公式更新 (ω，θ).
        7.   end for
        8. until 达到停止条件
    输出：(ω，θ) - 即相应的多层前馈神经网络.
----

Algorithms 2. 累积BP算法
----
    输入： 训练集 D，学习率 η，迭代次数 n.
    过程： 
        1. 随即初始化连接权与阈值 (ω，θ).
        2. Repeat：
        3.     根据当前参数计算出累积误差 E.
        4.     根据公式计算出标准梯度项 g.
        5.     根据公式更新 (ω，θ).
        6.     n = n-1
        7. until n=0 or 达到停止条件
    输出：(ω，θ) - 即相应的多层前馈神经网络.
----

可以看出，两种算法的本质区别类似于随机梯度下降法与标准梯度下降法的区别。pybrain包为我们实现这两种不同的算法提供了方便。我们只需要修改 pybrain.supervised.trainers 的初始化参数（如learningrate、batchlearning）并设置数据集遍历次数 trainEpochs() 即可。

数据预处理

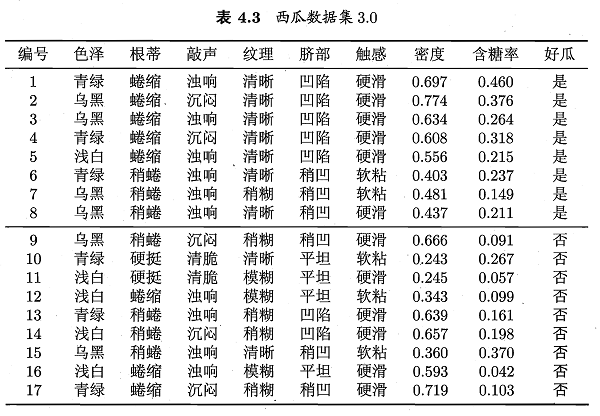
从表4.3的西瓜数据集3.0可以看到，样本共有8个属性变量和一个输出变量。其中既有标称变量（色泽~触感、好瓜），也有连续变量（密度、含糖率）。

为了方便进行神经网络模型的搭建（主要是为对离散值进行数值计算），首先考虑对标称变量进行数值编码，这里我们采用pandas.get_dummies()函数进行输入的独热编码（转化为哑变量的形式），采用pybrain.datasets.ClassificationDataSet的_convertToOneOfMany()进行输出的独热编码。关于独热编码
原理可参考One-hot_Wikipedia或数据预处理之独热编码（One-Hot Encoding）

对“西瓜数据集3.0”进行独热编码：

编码前：

编号  色泽  根蒂  敲声  纹理  脐部  触感     密度    含糖率 好瓜
0    1  青绿  蜷缩  浊响  清晰  凹陷  硬滑  0.697  0.460  是
1    2  乌黑  蜷缩  沉闷  清晰  凹陷  硬滑  0.774  0.376  是
2    3  乌黑  蜷缩  浊响  清晰  凹陷  硬滑  0.634  0.264  是
...

此时数据集大小[17,10]，8输入，1输出。

编码后：

编号     密度    含糖率  色泽_乌黑  色泽_浅白  色泽_青绿  根蒂_硬挺  根蒂_稍蜷  根蒂_蜷缩  敲声_沉闷  ...   \
0    1  0.697  0.460      0      0      1      0      0      1      0  ...    
1    2  0.774  0.376      1      0      0      0      0      1      1  ...    
2    3  0.634  0.264      1      0      0      0      0      1      0  ...   
...    

纹理_模糊  纹理_清晰  纹理_稍糊  脐部_凹陷  脐部_平坦  脐部_稍凹  触感_硬滑  触感_软粘  好瓜_否  好瓜_是  
0       0      1      0      1      0      0      1      0     0     1  
1       0      1      0      1      0      0      1      0     0     1  
2       0      1      0      1      0      0      1      0     0     1  
...

此时数据集大小[17,22]，19输入，2输出。

模型训练与测试

根据上面的数据，搭建一个19输入，2输出的前向反馈神经网络（BP network）。然后划分训练集与测试集，进行建模与验证实验。

实现说明，在pybrain中：splitWithProportion函数可直接划分数据；buildNetwork函数可用于搭建BP神经网络；BackpropTrainer用于生成训练模版并可基于此进行训练，改变相关参数可分别实现标准BP算法和累积BP算法；

生成模型，pybrain默认的是Sigmoid激活函数，其非常适用于二分类，另外还有一种激活函数十分适用于多分类（包括二分类），即Softmax function。这里我们将输出进行了独热编码，因此考虑采用Softmax作为输出层的激活函数，然后采用胜者通吃（winner-takes-all）法则确定分类结果。

模型生成样例代码：
1
2
n_h = 5 # hidden layer nodes number
net = buildNetwork(19, n_h, 2, outclass = SoftmaxLayer)

标准BP算法学习神经网络：

样例代码：

1 2	trainer = BackpropTrainer(net, trndata) trainer.trainEpochs(1)

累积BP算法学习神经网络样例代码（50次迭代）：

样例代码：
1
2
trainer = BackpropTrainer(net, trndata, batchlearning=True)
trainer.trainEpochs(50)
此外还可以绘制出累积BP算法参数学习过程的收敛曲线，查看详细代码：
两种算法比较：

上述两种BP算法实现的代码区别可参考PyBrain官网: trainers – - Supervised Training for Networks and other Modules

进行一次训练，然后基于测试集预测，得出两种方法的预测精度如下：
```
标准BP算法： epoch:    1  test error: 50.00%
累积BP算法：    epoch:   50  test error: 25.00%
```
可以看出，本次实验累积BP算法优于前者，但一次实验说服力不够，于是我们进行多次实验得出预测结果平均精度比较如下：
```
标准BP算法：
25.00%  75.00%  75.00%  75.00%  50.00%  50.00% ... 
average error rate: 47.50%

累积BP算法：
25.00%  75.00%  50.00%  50.00%  25.00%  50.00% ...
average error rate: 38.75%
```
从结果可以看出，累积BP算法精度总体还是优于标准BP算法。但在实验过程中我们注意到，累积BP算法的运行时间远大于标准BP算法。

进一步地，我们注意到，由于数据集限制（样本量太少），模型精度很差。

问题回顾

解题过程

算法分析

数据预处理

模型训练与测试

相关参考